LD A, (LOC1) LOAD CONTENTS OF LOC1 INTO A LD HL,LOC2 LOAD ADDRESS OF LOC2 INTO HL ADD A, (HL) ADD CONTENTS OF LOC2 TO CONTENTS OF LOC1 LD (LOC3), A STORE ACCUMULATOR INTO LOC3
Comparison: Conceptually, they are exactly the same.
LD A, (ADR1) LOAD LOW HALF OF OP1 LD HL, ADR2 ADDRESS OF LOW HALF OF OP2 ADD A, (HL) ADD OP1 AND OP2 LOW LD (ADR3), A STORE RESULT, LOW LD A, (ADR1+1) LOAD HIGH HALF OF OP1 INC HL ADDRESS OF HIGH HALF OF OP2 ADC A, (HL) (OP1 + OP2) HIGH + CARRY LD (ADR3+1), A STORE RESULT, HIGH
LD A, (ADR1-1) LOAD LOW HALF OF OP1 LD HL, ADR2-1 ADDRESS OF LOW HALF OF OP2 ADD A, (HL) ADD OP1 AND OP2 LOW LD (ADR3-1), A STORE RESULT, LOW LD A, (ADR1) LOAD HIGH HALF OF OP1 INC HL ADDRESS OF HIGH HALF OF OP2 ADC A, (HL) (OP1 + OP2) HIGH + CARRY LD (ADR3), A STORE RESULT, HIGH
LD A, (ADR1) LOAD LOWER HALF OF OP1 LD HL, ADR2 ADDRESS OF LOWER HALF OF OP2 SUB A, (HL) (OP1 - OP2) LOW LD (ADR3), A STORE RES, LOW LD A, (ADR1+1) LOAD HIGHER HALF OF OP1 INC HL ADDRESS OF HIGHER HALF OF OP2 SBC A, (HL) (OP1 - OP2) HIGH - CARRY LD (ADR3+1), A STORE RES, HIGH
LD A, (ADR1) LOAD OP1 LD HL, ADR2 ADDRESS OF OP2 SUB A, (HL) (OP1 - OP2) LD (ADR3), A STORE RES
In general, the result stored in (ADR) would not be a valid BCD value, because the correction by DAA was performed after the storage in the memory. So it could be done, but it would give a wrong result.
In this special case, however, the binary addition of "11" with "22" does not give an invalid BCD result, so if DAA were left out, it would not result in an invalid BCD result.
Exercise 3.10: LD A, (DE) instead of LD A,(ADR1).
Exercise 3.11: No, because there is no SBC A, (DE).
LD A, (ADR1) LOAD LOWER HALF OF OP1 LD HL, ADR2 ADDRESS OF LOWER HALF OF OP2 SUB A, (HL) (OP1 - OP2) LOW DAA DECIMAL ADJUST LD (ADR3), A STORE (RESULT) LOW LD A, (ADR1 + 1) LOAD HIGHER HALF OF OP1 INC HL POINT TO HIGHER HALF OF OP2 SBC A, (HL) (OP1 - OP2) HIGH - CARRY DAA DECIMAL ADJUST LD (ADR3 + 1), A STORE (RESULT) HIGH
Exercise 3.14: Very long routine:
MPY88 LD BC, (MPRAD)
LD DE, (MPDAD)
LD D, 0
LD HL, 0
BIT 0, C
JR NZ, NOADD0
ADD HL, DE
NOADD0 SLA E
RL D
BIT 1, C
JR NZ, NOADD1
ADD HL, DE
NOADD1 SLA E
RL D
BIT 2, C
JR NZ, NOADD2
ADD HL, DE
NOADD2 SLA E
RL D
BIT 3, C
JR NZ, NOADD3
ADD HL, DE
NOADD3 SLA E
RL D
BIT 4, C
JR NZ, NOADD4
ADD HL, DE
NOADD4 SLA E
RL D
BIT 5, C
JR NZ, NOADD5
ADD HL, DE
NOADD5 SLA E
RL D
BIT 6, C
JR NZ, NOADD6
ADD HL, DE
NOADD6 SLA E
RL D
BIT 7, C
JR NZ, NOADD7
ADD HL, DE
NOADD7 LD (RESAD), HL
Exercise 3.15: Yes, the routine would be 1 byte shorter, but 11 T states more to execute:
DEC B 1 BYTE, 8 X 4 T = 32 T } 123 T JR 2 BYTES, 7 X 12 T + 7 T = 91 T }
DEC B 1 BYTE, 8 X 4 T = 32 T } 112 T JP 3 BYTES, 8 X 10 T = 80 T }
Exercise 3.16: Yes, it would be 1 byte shorter, and 13 T states less to execute:
DEC B 1 BYTE, 8 X 4 T = 32 T } 112 T JP 3 BYTES, 8 X 10 T = 80 T }
DJNZ 2 BYTES, 7 X 13 T + 8 T = 99 T
Exercise 3.17: Yes, it is 1 byte shorter, and 1 T state less to execute.
Exercise 3.19: Speed makes no difference, because SLA E, RL D takes exactly as much clock cycles as SRL L, RR H.
Original program:
MPY88 LD BC, (MPRAD) LOAD MULTIPLIER INTO C
LD B, 8 B IS BIT COUNTER
LD DE, (MPDAD) LOAD MULTIPLICAND INTO E
LD D, 0 CLEAR D
LD HL, 0 SET RESULT TO 0
MULT SRL C SHIFT MULTIPLIER INTO CARRY
JR NC, NOADD TEST CARRY
ADD HL, DE ADD MPD TO RESULT
NOADD SLA E SHIFT MPD LEFT
RL D SAVE BIT IN D
DEC B DECREMENT SHIFT COUNTER
JP NZ, MULT DO IT AGAIN IF COUNTER <> 0
LD (RESAD), HL STORE RESULT
Alternative program:
MPY88A LD BC, (MPRAD) LOAD MULTIPLIER INTO C
LD B, 8 B IS BIT COUNTER
LD DE, (MPDAD) LOAD MULTIPLICAND INTO E
LD D, 0 CLEAR D
LD HL, 0 SET RESULT TO 0
MULT SRL C SHIFT MULTIPLIER INTO CARRY
JR NC, NOADD TEST CARRY
ADD HL, DE ADD MPD TO RESULT
NOADD SRL L SHIFT PARTIAL RES RIGHT
RR H SAVE BIT IN H
DEC B DECREMENT SHIFT COUNTER
JP NZ, MULT DO IT AGAIN IF COUNTER <> 0
LD (RESAD), HL STORE RESULT
Exercise 3.20: Original program used 504 T states, 252 us. The new program uses 384 T states, 192 us.
Original program:
MPY88 LD BC, (MPRAD) 20 T
LD B, 8 7 T
LD DE, (MPDAD) 20 T
LD D, 0 7 T
LD HL, 0 10 T
----- +
64 T
MULT SRL C -- 8 T
JR NC, NOADD -- 7 T / 12 T
ADD HL, DE -- 11 T
---- ----
26 T 20 T
NOADD SLA E -- 8 T
RL D -- 8 T
DEC B -- 4 T
JP NZ, MULT -- 10 T
---- ----
56 T 50 T
x 4 x 4
----- -----
224 T 200 T
------------ +
424 T
LD (RESAD), HL 16 T
----- +
504 T
New program:
MUL88C LD HL, (MPRAD-1) 20 T
LD L, 0 7 T
LD DE, (MPDAD) 20 T
LD D, 0 7 T
LD B, 8 7 T
----- +
61 T
MULT ADD HL, HL -- 11 T
JR NC, NOADD -- 7 T / 12 T
ADD HL, DE -- 11 T
---- ----
29 T 23 T
x 4 x 4
----- -----
116 T 92 T
------------ +
208 T
NOADD DJNZ MULT 99 T = 7 x 13 + 8
LD (RESAD), HL 16 T
----- +
384 T
MUL88D LD HL, (MPRAD-1) (same)
LD L, 0 (same)
LD BC, (MPDAD) (different)
LD B, 0 (different)
LD D, 8 (different)
MULT ADD HL, HL (same)
JR NC, NOADD (same)
ADD HL, BC (different)
NOADD DEC D (different)
JP NZ, MULT (different)
LD (RESAD), HL (same)
RET (same)
Exercise 3.22: It could destroy the multiplier MPR in register H, by adding another value than zero in register D.
Exercise 3.23: Advantage: All 16-bit numbers can be loaded in one instruction. Disadvantage: DJNZ is not possible, so the overall routine will be longer and slower.
MULT16A LD A, 16
LD BC, (MPRAD)
LD DE, (MPDAD)
LD HL, 0
MULT SRL C
RL B
JR NC, NOADD
ADD HL, DE
NOADD EX DE, HL
ADD HL, HL
EX DE, HL
DEC A
JP NZ, MULT
LD (RESAD), HL
RET
Exercise 3.24: The new code snippet is faster (by 3 T states), but results in longer code (1 byte longer).
New code snippet:
SLA E 2 BYTES, 8 T STATES } 16 T STATES
RL D 2 BYTES, 8 T STATES }
------- +
4 BYTES
Original code snippet:
EX DE, HL 1 BYTE, 4 T STATES }
ADD HL, HL 1 BYTE, 11 T STATES } 19 T STATES
EX DE, HL 1 BYTE, 4 T STATES }
------- +
3 BYTES
Exercise 3.25: The last carry indicates an overflow. However, if we test for a carry at the time RET is reached, the carry will be lost by the ADD HL, HL instruction. We have to save the carry before we test it with JR NC, NOADD, and then retrieve it before the loop is closed. Luckily DJNZ does not change the carry bit. To save the flag, we use PUSH AF, and to retrieve it, we use POP AF. The calling routine can now test for a set carry bit, which indicates an overflow error.
MUL16C LD A, (MPRAD + 1)
LD C, A
LD A, (MPRAD)
LD B, 16D
LD DE, (MPDAD)
LD HL, 0
MULT SRL C
RRA
PUSH AF SAVE CARRY FOR LATER
JR NC, NOADD TEST CARRY
ADD HL, DE
NOADD EX DE, HL
ADD HL, HL
EX DE, HL
POP AF RETRIEVE CARRY
DJNZ MULT
LD (RESAD), HL
RET IF CARRY IS SET AT THIS POINT,
AN OVERFLOW HAS OCCURRED. THE
CALLING ROUTINE HAS TO DEAL
WITH THAT
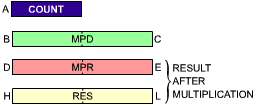
Exercise 3.26: The registers are used as follows (see Figure A3.1):
Fig. A3.1: Registers Used In Exercise 3.26
We want to use register pair DE to contain the high part of the 32-bit result. For this, we use the following diagram (see Figure A3.2):
Fig. A3.2: Data Flow Between Registers in Exercise 3.26
The multiplication loop MULT can be described as follows:
If after step 3, we do step 1, thus creating a program loop. The loop is ended if the value of register A reaches zero.
By rotating register E and then register D, the value of the carry is shifted into the right-most bit of register E, while the left-most bit of register D is shifted into the carry. This way, bit 16 of the result (coming out off register pair HL, and temporay stored in carry C) "shifts in" register pair DE on the right, while the multiplier MPR "shifts out" register pair DE on the left, into the carry bit.
Note, that we cannot use SLA E as in the answer of Exercise 3.24. We need to use a rotate instruction to shift the carry into the right-most bit of register E. SLA E would replace bit 16 of the result by a zero value. Remember, from the second iteration of the program loop on, the value of the carry bit at the start of the iteration originates from the ADD HL,HL instruction in the previous iteration of the program loop.
We have to combine the RL E instruction with a consecutive RL D instruction to shift the left-most bit of register D into the carry. We use this carry for testing purposes (to decide whether or not we should add MPD to RES), just as before.
Also note, when exiting the program loop, that the carry bit that resulted from the final ADD HL,HL operation is not yet shifted into register pair DE, as it should be. This means that the for a correct 32-bit result, we must perform this shift operation one more time.
The first time the two instructions "RL E/RL D" are executed (when the program loop is entered), the carry bit is undetermined. RL E rotates this undetermined carry bit into bit 0 of register E, and the combination "RL E/RL D" keeps left shifting this unwanted bit. After the program loop is exited, this bit is located in bit 7 of register D. However, the final "RL E/RL D" code sequence removes it from register D. (By the way, as a result, the original value of the C bit is preserved by this routine.)
MUL32 LD BC,(MPDAD) LOAD MPD FROM THE MEMORY
LD DE,(MPRAD) LOAD MPR FROM THE MEMORY
LD HL,0 INITIALIZE RES
LD A,16D COUNT 16 BITS
MULT RL E SHIFT IN CARRY FROM ADD HL,HL
RL D SHIFT OUT LEFT-MOST BIT OF MPR
JR NC,NOADD CHECK LEFT-MOST BIT OF MPR
ADD HL,BC ADD MPD TO RES
NOADD ADD HL,HL SHIFT LEFT RES
BIT 16 OF THE RESULT (PREVIOULY
BIT 7 OF REGISTER H) IS NOW
CONTAINED IN CARRY BIT C,
AND WILL BE SHIFTED INTO BIT 0
OF REGISTER E IN THE NEXT
ITERATION OF THE LOOP
DEC A DECREMENT COUNTER
JP NZ,MULT CONTINUE UNTIL COUNTER = 0
RL E SHIFT IN CARRY FROM ADD HL,HL
RL D
LD (RESAD),HL STORE INTO MEMORY LOWER PART
LD (RESAD+2),DE AND UPPER PART OF 32-BIT RES
The program suggested does not work. In the last iteration, both the quotient and remainder are doubled. This can't be right!
DIV168 LD A,(DVSAD) LOAD DIVISOR
LD D,A INTO D
LD E,0
LD HL,(DVDAD) LOAD 16-BIT DIVIDEND
LD B,8 INITIALIZE COUNTER
DIV XOR A CLEAR C BIT
SBC HL,DE DIVIDEND - DIVISOR
INC HL QUOTIENT = QUOTIENT + 1
JP P,NOADD TEST IF REMAINDER
POSITIVE
ADD HL,DE RESTORE IF NECESSARY
DEC HL QUOTIENT = QUOTIENT - 1
NOADD ADD HL,HL SHIFT DIVIDEND LEFT
DJNZ DIV LOOP UNTIL B = 0
In fact, there has to be a little piece of code added to this routine (between DJNZ DIV and RET) to make it right:
XOR A CLEAR CARRY C
SBC HL,DE FINAL TRIAL-SUBTRACT
INC HL INCREMENT QUOTIENT
JP P,EXIT DON'T ADD IF POSITIVE
ADD HL,DE CORRECT REMAINDER IN H
DEC HL DECREMENT QUOTIENT IN L
EXIT RET
To test the validity of this program, let us divide 320 (0140H) by 7 (07H), and fill out the form below (contents (DE) = 0700H). If you check the table in Figure A3.3, you will see that H and L contain the correct result--H contains the remainder "05H" (5 in decimal), and L the quotient "2DH" (45 in decimal). You may confirm that if we had not performed the additional steps (exclude the light-blue colored rows in Figure A3.3), the result would have been: remainder (H) = 0CH (=12 decimal), quotient (L) = 2CH (=44 decimal).
Note, that if the dividend is greater than (16383 + divisor), i.e., if bit 15 of register pair HL is set, the sign flag M will always be set if the divisor is less than 128 (which means that bit 15 of register pair DE is cleared), and the result will be wrong. Something similar applies to the situation that the divisor is larger than 127, and the dividend less than 16384.
This means that both the divisor and dividend should be positive numbers in the two's complement notation. In fact, this is a 15/7 division, and not a 16/8 division program.
| LABEL | INSTRUCTION | B | H | L |
|---|---|---|---|---|
| DIV168 | LD A,(DVSAD) | -- | -- | -- |
| LD D,A | -- | -- | -- | |
| LD E,0 | -- | -- | -- | |
| LD HL,(DVDAD) | -- | 01 | 40 | |
| LD B,8 | 08 | 01 | 40 | |
| DIV | XOR A | 08 | 01 | 40 |
| SBC HL,DE | 08 | FA | 40 | |
| INC HL | 08 | FA | 41 | |
| JP P,NOADD | 08 | FA | 41 | |
| ADD HL,DE | 08 | 01 | 41 | |
| DEC HL | 08 | 01 | 40 | |
| NOADD | ADD HL,HL | 08 | 02 | 80 |
| DJNZ DIV | 07 | 02 | 80 | |
| DIV | XOR A | 07 | 02 | 80 |
| SBC HL,DE | 07 | FB | 80 | |
| INC HL | 07 | FB | 81 | |
| JP P,NOADD | 07 | FB | 81 | |
| ADD HL,DE | 07 | 02 | 81 | |
| DEC HL | 07 | 02 | 80 | |
| NOADD | ADD HL,HL | 07 | 05 | 00 |
| DJNZ DIV | 06 | 05 | 00 | |
| DIV | XOR A | 06 | 05 | 00 |
| SBC HL,DE | 06 | FE | 00 | |
| INC HL | 06 | FE | 01 | |
| JP P,NOADD | 06 | FE | 01 | |
| ADD HL,DE | 06 | 05 | 01 | |
| DEC HL | 06 | 05 | 00 | |
| NOADD | ADD HL,HL | 06 | 0A | 00 |
| DJNZ DIV | 05 | 0A | 00 | |
| DIV | XOR A | 05 | 0A | 00 |
| SBC HL,DE | 05 | 03 | 00 | |
| INC HL | 05 | 03 | 01 | |
| JP P,NOADD | 05 | 03 | 01 | |
| NOADD | INC HL,HL | 05 | 06 | 02 |
| DJNZ DIV | 04 | 06 | 02 | |
| DIV | XOR A | 04 | 06 | 02 |
| SBC HL,DE | 04 | FF | 02 | |
| INC HL | 04 | FF | 03 | |
| JP P,NOADD | 04 | FF | 03 | |
| ADD HL,DE | 04 | 06 | 03 | |
| DEC HL | 04 | 06 | 02 | |
| NOADD | ADD HL,HL | 04 | 0C | 04 |
| DJNZ DIV | 03 | 0C | 04 | |
| DIV | XOR A | 03 | 0C | 04 |
| SBC HL,DE | 03 | 05 | 04 | |
| INC HL | 03 | 05 | 05 | |
| JP P,NOADD | 03 | 05 | 05 | |
| NOADD | ADD HL,HL | 03 | 0A | 0A |
| DJNZ DIV | 02 | 0A | 0A | |
| DIV | XOR A | 02 | 0A | 0A |
| SBC HL,DE | 02 | 03 | 0A | |
| INC HL | 02 | 03 | 0B | |
| JP P,NOADD | 02 | 03 | 0B | |
| NOADD | INC HL,HL | 02 | 06 | 16 |
| DJNZ DIV | 01 | 06 | 16 | |
| DIV | XOR A | 01 | 06 | 16 |
| SBC HL,DE | 01 | FF | 16 | |
| INC HL | 01 | FF | 17 | |
| JP P,NOADD | 01 | FF | 17 | |
| ADD HL,DE | 01 | 06 | 17 | |
| DEC HL | 01 | 06 | 16 | |
| NOADD | INC HL,HL | 01 | 0C | 2C |
| DJNZ DIV | 00 | 0C | 2C | |
| XOR A | 00 | 0C | 2C | |
| SBC HL,DE | 00 | 05 | 2C | |
| INC HL | 00 | 05 | 2D | |
| JP P,EXIT | 00 | 05 | 2D | |
| EXIT | RET | 00 | 05 | 2D |
Fig. A3.3: Complete Trace of 16/8 Division Program
(the additional steps are colored light-blue)