The purpose of this chapter is to present the basic techniques necessary in order to write a program using the Z80. This chapter will introduce new concepts such as register management, loops, and subroutines. It will focus on programming techniques using only the internal Z80 resources, i.e., the registers. Actual programs will be developed, such as arithmetic programs. These programs will serve to illustrate the various concepts presented so far and will use actual instructions. Thus, it will be seen how instructions may be used to manipulate the information between memory and the MPU, as well as to manipulate information within the MPU itself. The next chapter will then discuss in complete detail the instructions available on the Z80. Chapter 5 will present Addressing Techniques, and Chapter 6 will present the techniques available for manipulating information outside the Z80: the Input/Output Techniques.
In this chapter, we will essentially learn by "doing." By examining programs of increasing complexity, we will learn the role of the various instructions, of the registers, and we will apply the concepts developed so far. However, one important concept will not be presented here; it is the concept of addressing techniques. Because of its apparent complexity, it will be presented separately in Chapter 5.
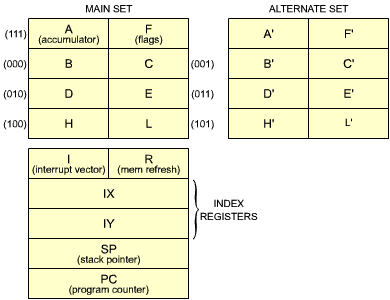
Let us immediately start writing down some programs for the Z80. We will start with arithmetic programs. The "programmer's model" of the Z80 register is shown in Figure 3.0.
Fig. 3.0: The Z80 Registers
Arithmetic programs include addition, subtraction, multiplication, and division. The programs presented here will operate on integers. These integers may be positive binary integers or may be expressed in two's complement notation, in which case the left-most bit is the sign bit (see Chapter 1 for a description of the two's complement notation).
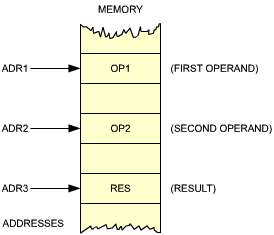
Fig. 3.1: Eight-Bit Addition RES = OP1 + OP2
We will add two 8-bit operands called OP1 and OP2, respectively stored at memory address ADR1, and ADR2. The sum will be called RES and will be stored at memory address ADR3. This is illustrated in Figure 3.1. The program which will perform this addition is the following:
Instructions Comments LD A,(ADR1) LOAD OP1 INTO A LD HL,ADR2 LOAD ADDRESS OF OP2 INTO HL ADD A,(HL) ADD OP2 TO OP1 LD (ADR3),A SAVE RESULT RES AT ADR3
This is our first program. The instructions are listed on the left and comments appear on the right. Let us now examine the program. It is a four-instruction program. Each line is called an instruction and is expressed here in symbolic form. Each such instruction will be translated by the assembler program into one, two, three or four binary bytes. We will not concern ourselves here with the translation and will only look at the symbolic representation.
The first line specifies loading the contents of ADR1 into the accumulator A. Referring to Figure 3.1, the contents of ADR1 are the first operand, "OP1". This first instruction therefore results in transferring OP1 from the memory into the accumulator. This is shown in Figure 3.2. "ADR1" is a symbolic representation for the actual 16-bit address in the memory. Somewhere else in the program, the ADR1 symbol will be defined. It could, for example, be defined as being equal to the address "100".
Fig. 3.2: LD A, (ADR1): OP1 is Loaded from Memory
This load instruction will result in a read operation from address 100 (see Figure 3.2), the contents of which will be transferred along the data bus and deposited inside the accumulator. You will recall from the previous chapter that arithmetic and logical operations operate on the accumulator as one of the source operands. (Refer to the previous chapter for more details.) Since we wish to add the two values OP1 and OP2 together, we must first load OP1 into the accumulator. Then, we will be able to add the contents of the accumulator, i.e., add OP1 to OP2. The right-most field of this instruction is called a comment field. It is ignored by the assembler program at translation time, but is provided for program readability. In order to understand what the program does, it is of paramount importance to use good comments. This is called documenting a progam.
Here the comment is self-explanatory: the value of OP1, which is located at address ADR1, is loaded into the accumulator A.
The result of this first instruction is illustrated by Figure 3.2. The second instruction of our progam is:
LD HL, ADR2
It specifies: "Load ADR2 into registers H and L." In order to read the second operand, OP2, from memory, we must first place its address into a register pair of the Z80, such as H and L. Then, we can add the contents of the memory location whose address is in H and L to the accumulator.
ADD A, (HL)
Referring to Figure 3.1, the contents of memory location ADR2 are OP2, our second operand. The contents of the accumulator are now OP1, our first operand. As a result of the execution of this instruction, OP2 will be fetched from the memory and added to OP1. This is illustrated in Figure 3.3.
Fig. 3.3: ADD A, (HL)
The sum will be deposited in the accumulator. The reader will remember that, in the case of the Z80, the results of the arithmetic operations are deposited back into the accumulator. In other processors, it may be possible to deposit these results in other registers, or back into the memory.
The sum of OP1 and OP2 is now contained in the accumulator. To complete our program, we simply have to transfer the contents of the accumulator into memory location ADR3, in order to store the results at the specified location. This is performed by the fourth instruction of our program:
LD (ADR3), A
This instruction loads the contents of A into the specified address ADR3. The effect of this final instruction is illustrated by Figure 3.4.
Fig. 3.4: LD (ADR3), A (Save Accumulator in Memory)
Before execution of the ADD operation, the accumulator contained OP1 (see Figure 3.3). After the addition, a new result has been written into the accumulator. It is "OP1 + OP2". Recall that the contents of any register within the microprocessor, as well as any memory location, remain the same after a read operation has been performed on this register. In other words, reading the contents of a register or memory location does not change its contents. It is only, and exclusively, a write operation into this register location that will change its contents. In this example, the contents of memory location ADR1 and ADR2 remain unchanged throughout the program. However, after the ADD instruction, the contents of the accumulator will have been modified, because the output of the ALU has been written into the accumulator. The previous contents of A are then lost.
Actual numerical addresses may be used instead of ADR1, ADR2, and ADR3. In order to keep symbolic addresses, it will be necessary to use so-called "pseudo-instructions" which specify the value of these symbolic addresses, so that the assembly program may, during translation, substitute the actual physical addresses. Such pseudo-instructions could be, for example:
ADR1 = 100H ADR2 = 120H ADR3 = 200H
An 8-bit addition will only allow the addition of 8-bit numbers, i.e., numbers between 0 and 255, if absolute binary is used. For most practical applications it is necessary to add numbers having 16 bits or more, i.e., to use multiple precision. We will here present examples of arithmetic on 16-bit numbers. They can be readily extended to 24, 32 bits or more (always multiples of 8 bits). We will assume that the first operand is stored at memory locations ADR1 and ADR1-1. Since OP1 is a 16 bit number this time, it will require two 8-bit memory locations. Similarly, OP2 will be stored at ADR2 and ADR2-1. The result is to be deposited at memory addresses ADR3 and ADR3-1. This is illustrated in Figure 3.5. H indicates the high half (bits 8 through 15), while L indicates the low half bits (bits 0 through 7).
Fig. 3.5: 16-Bit Addition - The Operands
The logic of the program is exactly like the previous one. First, the lower half of the two operands will be added, since the microprocessor can only add on 8 bits at a time. Any carry generated by the addition of these low order bytes will automatically be stored in the internal carry bit ("C"). Then, the high order half of the two operands will be added together along with any carry, and the result will be saved in the memory. The program appears below:
LD A,(ADR1) LOAD LOW HALF OF OP1 LD HL,ADR2 ADDRESS OF LOW HALF OF OP2 ADD A,(HL) ADD OP1 AND OP2 LOW LD (ADR3),A STORE RESULT, LOW LD A,(ADR1-1) LOAD HIGH HALF OF OP1 DEC HL ADDRESS OF HIGH HALF OF OP2 ADC A,(HL) (OP1 + OP2) HIGH + CARRY LD (ADR3-1),A STORE RESULT, HIGH
The first four instructions of this program are identical to the ones used for the 8-bit addition in the previous section. They result in adding the least significant halves (bits 0-7) of OP1 and OP2. The sum, called "RES" is stored at memory location ADR3 (see Figure 3.5).
Automatically, whenever an addition is performed, any resulting carry (whether "0" or "1") is saved in the carry bit C of the flags register (register F). If the two numbers do generate a carry, the the C bit will be equal to "1" (it will be set). If the two 8-bit numbers do not generate any carry, the value of the carry bit will be "0".
The next four instructions of the program are essentially like those used in the previous 8-bit addition program. This time they add together the most significant half (or high half, i.e., bits 8-15) of OP1 and OP2, plus any carry, and store the result at address ADR3-1.
After execution of this 8-instruction program, the 16-bit result is stored at memory locations ADR3 and ADR3-1, as specified. Note, however, that there is one difference between the second half of this program and the first half. The "ADD" instruction which has been used is not the same as in the first half. In the first half of this program (the 3rd instruction), we had used the "ADD" instruction. This instruction adds the two operands, regardless of the carry. In the second half, we use the "ADC" instruction, which adds the two operands together, plus any carry that may have been generated. This is necessary in order to obtain the correct result. The addition initially performed on the low operands many result in a carry. Such a possible carry must be taken into account in the second half of the addition.
The question which comes naturally then is: what if the addition of the high half of the operands also results in a carry? There are two possibilities: the first one is to assume this is an error. This program is then designed to work for results up to 16 bits, but not 17. The other one is to include additional instructions to test explicitly for the possibility of a carry at the end of this program. This is a choice which the programmer must make, the first of many choices.
Note: We have assumed here that the high part of the operand is stored "on top of" the lower part, i.e., at the lower memory address. This need not be the case. In fact, addresses are stored by the Z80 in the reverse manner: the low part is first saved in the memory, and the high part is saved in the next memory location. In order to use a common convention for both addresses and data, it is recommended that data also be kept with the low part on top of the high part. This is illustrated in Figure 3.6.
Fig. 3.6: Storing Operands in Reverse Order
When operating on multiple operands, it is important to keep in mind two essential conventions:
Exercises 3.2 and 3.3 are designed to clarify this point
| Exercise 3.2: |
Rewrite the 16-bit addition program above with the memory lay-out indicated in Figure 3.6. |
| Exercise 3.3: |
Assume now that ADR1 does not point to the lower half of OP1 (as in Figure 3.5 and 3.6), but points to the higher part of OP1. This is illustrated in Figure 3.7. Again, write the corresponding program.
Fig. 3.7: Pointing to the High Byte |
It is the programmer, i.e., you, who must decide how to store 16-bit numbers (i.e., lower part or higher part first) and also whether your address references point to the lower or the higher half of such numbers. This is another choice which you will learn to make when designing algorithms or data structures.
The programs presented here are traditional programs, using the accumulator. We will now present an alternative program for the 16-bit addition that does not use the accumulator, but instead uses some of the special 16-bit instructions available on the Z80. Operands will be assumed to be stored as indicated in Figure 3.5. The program is:
LD HL,(ADR1) LOAD HL WITH OP1 LD BC,(ADR2) LOAD BC WITH OP2 ADD HL,BC ADD 16 BITS LD (ADR3),HL STORE RES INTO ADR3
Note how much shorter this program is, compared to our previous version. It is more "elegant." In a limited manner, the Z80 allows registers H and L to be used as a 16-bit accumulator.
| Exercise 3.4: | Using the 16-bit instructions which have just been introduced, write an addition program for 32-bit operands, assuming that operands are stored as shown in Figure 3.8. (The answer appears below.)
Fig. 3.8: A 32-Bit Addition |
| Answer: | LD HL,(ADR1) LD BC,(ADR2) ADD HL,BC LD (ADR3),HL LD HL,(ADR1+2) LD BC,(ADR2+2) ADC HL,BC LD (ADR3+2),HL |
Now that we have learned to perform a binary addition, let us turn to subtraction.
Doing an 8-bit subtract would be too simple. Let us keep it as an exercise and directly perform a 16-bit subtract. As usual, our two numbers, OP1 and OP2, are stored at addresses ADR1 and ADR2. The memory layout will be assumed to be that of Figure 3.6. In order to subtract, we will use a subtract operation (SBC) instead of an add operation (ADD).
| Exercise 3.5: | Now write a subtraction program.
The program appears below. The data paths are shown in Figure 3.9. LD HL,(ADR1) OP1 INTO HL LD DE,(ADR2) OP2 INTO BC AND A CLEARY CARRY SBC HL,DE OP1 - OP2 LD (ADR3),HL RES INTO ADR3 Fig. 3.9: 16-Bit Load - LD HL,(ADR1) |
This program is essentially like the one developed for 16-bit addition. However, the Z80 instruction-set has two types of addition on double registers: ADD and ADC, but only one type of subtraction: SBC.
As a result, two changes can be noted.
A first change is the use of SBC instead of ADD.
The other change is the "AND A" instruction, used to clear the carry flag prior to the subtraction. This instruction does not modify the value of A.
This precaution is necessary because the Z80 is equipped with two modes of addition, with and without carry on the H and L registers, but with only one mode of subtraction, the SBC instruction of "subtract with carry" when operating on the HL register pair. Because SBC automatically takes into account the value of the carry bit, it must be set to 0 prior to starting the subtraction. This is the role of the "AND A" instruction.
| Exercise 3.6: |
Rewrite the subtraction program without using the specialized 16-bit instruction. |
| Exercise 3.7: |
Write the subtraction program for 8-bit operands. |
It must be remembered that in the case of two's complement arithmetic, the final value of the carry flag has no meaning. If an overflow condition has occurred as a result of the subtraction, then the overflow bit (bit V) of the flags register will have been set. It can then be tested.
The examples just presented are simple binary additions or subtractions. However, another type of arithmetic may be necessary; it is BCD arithmetic.
The concept of BCD arithmetic has been presented in Chapter 1. Let us recall its features. It is essentially used for business applications where it is imperative to retain every significant digit in a result. In the BCD notation, a 4-bit nibble is used to store one decimal digit (0 through 9). As a result, every 8-bit byte may store two BCD digits. (This is called packed BCD). Let us now add two bytes each containing two BCD digits.
In order to identify the problems, let us try some numeric examples first.
Let us add "01" and "02":
"01" is represented by: 0000 0001
"02" is represented by: 0000 0010
---------
The result is: 0000 0011
This is the BCD representation for "03". (If you feel unsure of the BCD equivalent, refer to the conversion table at the end of this book.) Everything worked very simple in this case. Let us now try another example.
"08" is represented by: 0000 1000 "03" is represented by: 0000 0011
The problem stems from the fact that the BCD representation uses only the first ten combinations of 4 digits in order to encode the decimal symbols 0 through 9. The remaining six possible combinations of 4 digits are unused, and the illegal "1011" is one such combination. In other words, whenever the sum of two BCD digit is greater than 9, then one must add 6 to the result in order to skip over the 6 unused codes.
Add the binary representation of "6" to "1011":
1011 (illegal binary result)
+ 0110 (+6)
---------
The result is: 0001 0001
This is, indeed, "11" in the BCD notation! We now have the correct result.
This example illustrates one of the basic difficulties of the BCD mode. One must compensate for the six missing codes. A special instruction, "DAA", called "decimal adjust," must be used to adjust the result of the binary addition. (Add 6 if the result is greater than 9.)
The next problem is illustrated by the same example. In our example, the carry will be generated from the lower BCD digit (the right-most one) into the left-most one. This internal carry must be taken into account and added to the second BCD digit. The addition instruction takes care of this automatically. However, it is often convenient to detect the internal carry from bit 3 to bit 4 (the "half-carry"). The H flag is provided for this purpose.
As an example, here is a program to add the BCD numbers "11" and "22":
LD A,11H LOAD LITERAL BCD "11" ADD A,22H ADD LITERAL BCD "22" DAA DECIMAL ADJUST RESULT LD (ADR),A STORE RESULT
In this program, we are using a new symbol "H". The "H" sign within the operand field of the instruction specifies that the data it follows is expressed in hexadecimal notation. The hexadecimal and the BCD representation for digit "0" through "9" are identical. Here we wish to add the literals (or constants) "11" and "22". The result is stored at the address ADR. When the operand is specified as part of the instruction, as it is in the above example, the is called immediate addressing. (The various addressing modes will be discussed in detail in Chapter 5.) Storing the result at a specified address, such as LD (ADR), A is called absolute addressing when ADR represents a 16-bit address.
Fig. 3.10: Storing BCD Digits
This program is analogous to the 8-bit binary addition, but uses a new instruction: "DAA". Let us illustrate its role in an example. We will first add "11" and "22" in BCD:
00010001 (11) + 00100010 (22) -------- = 00110011 \--/\--/ 3 3
The result is correct, using the rules of binary addition.
Let us now add "22" and "39", by using the rules of binary addition:
00100010 (22) + 00111001 (39) -------- = 01011011 \--/\--/ 5 ?
"1011" is an illegal BCD code. This is because BCD uses only the first 10 binary codes, and "skips over" the next 6. We must do the same, i.e. add 6 to the result:
01011011 (binary result) + 00000110 (6) -------- 01100001 (61) \--/\--/ 6 1
This is the correct BCD result.
| Exercise 3.9: |
Could we move the DAA instruction in the program after the instruction LD (ADR), A? |
BCD subtraction is, in appearance, complex. In order to perform a BCD subtraction, one must add the tens complement of the number, just as one adds the two's complement of a number to perform a binary subtract. The ten's complement is obtained by computing the complement to 9, then adding "1". This requires typically three to four operations on a standard microprocessor. However, the Z80 is equipped with a powerfull DAA instruction which simplifies the program.
The DAA instruction automatically adjusts the value of the result in the accumulator, depending on the value of the C, H and N flags before DAA, to the correct value. (See the next chapter for more details on DAA.)
16-bit addition is performed just as simply as in the binary case. The program for such an addition appears below:
LD A,(ADR1) LOAD (OP1) L INTO A LD HL,ADR2 LOAD ADR2 INTO HL ADD A,(HL) (OP1 + OP2) LOW DAA DECIMAL ADJUST LD (ADR3),A STORE (RESULT) LOW LD A,(ADR1+1) LOAD (OP1) H INTO A INC HL POINT TO ADR2 + 1 ADC A,(HL) (OP1 + OP2) HIGH + CARRY DAA DECIMAL ADJUST LD (ADR3+1),A STORE (RESULT) HIGH
Elementary BCD addition and subtraction have been described. However, in actual practice, BCD numbers include any number of bytes. As a simplified example of a packed BCD subtract, we will assume that the two numbers located at N1 and N2 include the same number of BCD bytes. The number of bytes is called COUNT. The register and memory allocation is shown in Figure 3.11. The program appears below:
BCDPAK LD B,COUNT
LD DE,N2
LD HL,N1
AND A CLEAR CARRY
MINUS LD A,(DE) N2 BYTE
SBC A (HL) N2 - N1
DAA
LD (HL),A STORE RESULT
INC DE
INC HL
DJNZ MINUS DEC B, LOOP UNTIL B = 0
Fig. 3.11: Packed BCD Subtract: N1 ![]() N2-N1
N2-N1
N1 and N2 represent the address where the BCD numbers are stored. These addresses will be loaded in register pairs DE and HL:
BCDPAK LD B,COUNT
LD DE,N2
LD HL,N1
Then, in anticipation of the first subtraction, the carry bit must be cleared. It has been pointed out that the carry bit can be cleared in a number of equivalent ways. Here, for example, we use:
AND A
The first byte of N2 is loaded into the accumulator, then the first byte of N1 is subtracted from it. The DAA instruction is then used, to obtain the correct BCD value:
MINUS LD A,(DE) N2 BYTE
SBC A,(HL) N2 - N1
DAA
The result is then stored into N1:
LD (HL),A
Finally, the pointers to the current byte are incremented:
INC DE
INC HL
The counter is decremented and the subtraction loop is executed until it reaches the value "0":
DJNZ MINUS
The DJNZ instruction is a special Z80 instruction which decrements register B and jumps if it is not zero, in a single instruction.
| Exercise 3.10: |
Compare the program above to the one for the 16-bit binary addition. What is the difference? |
| Exercise 3.11: |
Can you exchange the roles of DE and HL? (Hint: Be carefull with SBC.) |
| Exercise 3.12: |
Write the subtraction program for a 16-bit BCD. |
In BCD mode, the carry flag set as the result of an addition indicates the fact that the result is larger than 99. This is not like the two's complement situation, since BCD digits are represented in true binary. Conversely, the presence of the carry flag after a subtraction indicates a borrow.
We have now used two types of microprocessor instructions. We have used LD, which loads the accumulator from the memory address, or stores its contents at the specified address. This is a data transfer instruction.
Next, we have used arithmetic instructions, such as ADD, SUB, ADC and SBC. They perform addition and subtraction operations. More ALU instructions will be introduced soon in this chapter.
Still other types of instructions are available within the microprocessor which we have not used yet. They are in particular "jump" instructions, which will modify the order in which the program is being executed. This new type of instruction will be introduced in our next example. Note that jump instructions are often called "branch" for conditional situations, i.e., instances where there is a logical choice in the program. The "branch" derives its name from the analogy to a tree, and implies a fork in the representation of the program.
Let us now examine a more complex arithmetic problem: the multiplication of binary numbers. In order to introduce the algorithm for a binary multiplication, let us start by examining a usual decimal multiplication: We will multiply 12 by 23.
12 (Multiplicand) × 23 (Multiplier) ------ 36 (Partial Product) + 24 ------ = 276 (Final Result)
The multiplication is performed by multiplying the right-most digit of the multiplier by the multiplicand, i.e., "3" × "12". The partial product is "36". Then one multiplies the next digit of the multiplier, i.e., "2", by "12". "24" is then added to the partial product.
But there is one more operation: 24 is offset to the left by one position. We will say 24 is shifted left by one position. Equivalently, we could have said that the partial product (36) had been shifted one position to the right before adding.
The two numbers, correctly shifted, are then added and the sum is 276. This is simple. The binary multiplication is performed in exactly the same way.
Let us look at an example. We will multiply 5 × 3:
(5) 101 (MPD)
(3) 011 (MPR)
-------
101
101
000
-------
(15) 01111 (RES)
In order to perform the multiplication, we operate exactly as we did above. The formal representation of this algorithm appears in Figure 3.12. It is a flowchart for the algorithm, our first flowchart. Let us examine it more closely.
Fig. 3.12: The Basic Multiplication Algorithm - Flowchart
This flowchart is a symbolic representation of the algorithm we have just presented. Every rectangle represents an order to be carried out. It will be translated into one or more program instructions. Every diamond-shaped symbol represents a test being performed. This will be a branching point in the program. If the test succeeds, we will branch to another location. The concept of branching will be explained later, in the program itself. The reader should now examine the flowchart and ascertain that it does indeed exactly represent the algorithm which has been presented. Note that there is an arrow coming out of the last diamond at the bottom of the flowchart, back to the first diamond on top. This is because the same portion of the flowchart will be executed eight times, once for every bit of the multiplier. Such a situation, where execution will restart at the same point, is called a program loop for obvious reasons.
Let us now translate this flowchart into a program for the Z80. The complete program appears in Figure 3.13. We are going to study it in detail. As you will recall from Chapter 1, programming consists here of translating the flowchart of Figure 3.12 into a program of Figure 3.13. Each of the boxes in the flowchart will be translated by one or more instructions.
It is assumed that MPR and MPD already have a value.
MPY88 LD BC,(MPRAD) LOAD MULTIPLIER INTO C
LD B,8 B IS BIT COUNTER
LD DE,(MPDAD) LOAD MULTIPLICAND INTO E
LD D,0 CLEAR D
LD HL,0 SET RESULT TO 0
MULT SRL C SHIFT MULTIPLIER INTO CARRY
JR NC,NOADD TEST CARRY
ADD HL,DE ADD MPD TO RESULT
NOADD SLA E SHIFT MPD LEFT
RL D SAVE BIT IN D
DEC B DECREMENT SHIFT COUNTER
JP NZ,MULT DO IT AGAIN IF COUNTER <> 0
LD (RESAD),HL STORE RESULT
Fig. 3.13: 8 × 8 Multiplication Program
The first box of the flowchart is an initialization box. It is necessary to set a number of registers or memory locations to "0", as this program will require their use. The registers which will be used by the multiplication program appear in Figure 3.14.
Fig. 3.14: 8 × 8 Multiplication - The Registers
Three register pairs of the Z80 are used for the multiplication program. The 8-bit multiplier is assumed to reside at memory address MPRAD. The multiplicand MPD is assumed to reside at memory address MPDAD. The multiplier and the multiplicand respectively will be loaded into register C and E (see Figure 3.14). Register B will be used as a counter.
Register D and E will hold the multiplicand as it is shifted left on bit at a time.
Note that, even though only C and E need to be loaded initially, a 16-bit load must be used, so that B and D will also be loaded from memory, and will have to be reset respectively to "8" and to "0".
Finally, the results of an 8-bit multiplication may require up to 16 bits. This is because 28 × 28 = 216. Two registers must therefore be reserved for the result. They are registers H and L, as indicated in Figure 3.14.
The first step is to load register B, C, and E with the appropriate contents, and to initialize the result (the partial product) to the value "0" as specified by the flowchart of Figure 3.12. This is accomplished by the following instructions:
MPY88 LD BC,(MPRAD)
LD B,8
LD DE,(MPDAD)
LD D,0
LD HL,0
The first three instructions respectively load MPR into register pair BC, the value "8" into register B, and MPD into register pair DE. Since MPR and MPD are only 8-bit words, they are, in fact, loaded into register C and E respectively, while the next words in the memory after MPR and MPD get loaded into B and D. This is shown in Figure 3.15 and 3.16. The next instruction will zero the contents of D
Fig. 3.15: LD BC, (MPRAD)
Fig. 3.16: LD DE, (MPDAD)
In this multiplication program, the multiplicand will be shifted left before being added to the result (remember that, optionally, it is possible to shift the result to the right instead, as indicated in the fourth box in the flowchart of Figure 3.12). The multiplicand MPD will be shifted into register D at each step. This register D must therefore be initialize to the value "0". This is accomplished by the fourth instruction. Finally, the fifth instruction sets the contents of registers H and L to 0 in a single instruction.
Referring back to the flowchart of Figure 3.12, the next step is to test the least significant bit (the right-most bit) of the multiplier MPR. If this bit is a "1", then the value of MPD must be added to the partial result, otherwise it will not be added. This is accomplished by the next three instructions:
MULT SRL C
JR NC,NOADD
ADD HL,DE
The first problem we must solve is how to test the least significant bit of the multiplier, contained in register C. We could here use the BIT instruction of the Z80, which allows testing any bit in any register. However, in this case, we would like to construct a program as simple as possible, using a loop. If we were using the BIT instruction here, we would first test bit 0, then later bit 1, and so on until we reached bit 7. This would require a different instruction every time, and a simple loop could not be used. In order to shorten the length of the program, we must use a different instruction. Here we are using a shift instruction.
Note: There is a way to use the BIT instruction and a loop, but that would require the program to modify itself, a practice we will avoid.
SRL is a new type of operation within the arithmetic and logical unit. It stands for "shift right logical". A logical shift to the right is characterized by the fact that a "0" comes into bit position 7. This can be contrasted to an arithmetic shift to the right, where the bit coming into position 7 is identical to the previous value of bit 7. The different types of shift operations will be described in the next chapter. The effect of the SRL C instruction is illustrated in Figure 3.14 by an arrow coming out of register C and into the square used to designate the carry bit (also called "C"). At this point, the right-most bit of MPR will be in the carry bit C, where it can be tested.
Fig. 3.17: Shift and Rotate
The next instruction, "JR NC, NOADD", is a jump operation. It means "jump on no carry" (NC) to the address (the label) NOADD. If the contents of the carry bit are "0" (no carry), then the program will jump to the address NOADD. If the contents of C are "1" (the carry bit is set), then no branch will occur, and the next sequential instruction will be executed, i.e., the instruction "ADD HL,DE" will be executed.
This instruction specifies that the contents of D and E be added to H and L, with the result in H and L. Since E contains the multiplicand MPD (see Figure 3.14), this adds the multiplicand to the partial result.
At this point, regardless of whether MPD has been added to the result or not, the multiplicand must be shifted left (this is the fourth box in the flowchart of Figure 3.12). This is accomplished by:
NOADD SLA E
SLA stands for "shift left arithmetic." It has just been explained above that there are two types of shift operations, a logical shift and an arithmetic shift. This is the arithmetic one. In the case of a left shift, an SLA specifies that the bit coming into the right part of the register (the least significant bit) be a "0" (just as in the case of an SRL before).
As an example, let us assume that the intial contents of register E were 00001001. After the SLA instruction, the contents of E will be 00010010. And the contents of the carry bit will be 0.
However, looking back at Figure 3.14, we really want to shift the most significant bit (called MSB) of E directly into D (this is illustrated by the arrow on the illustration coming from E into D). However, there is no instruction which will shift a double register such as D and E in one operation. Once the contents of E have been shifted, the left-most bit has "fallen into" the carry bit. We must collect this bit from the carry bit and shift it into register D. This is accomplished by the next instruction:
RL D
RL is still another type of shift operation. It stands for "rotate left." In a rotation operation, as opposed to a shift operation, this bit coming into the register is the contents of the carry bit C (see Figure 3.17). This is exactly what we want. The contents of the carry bit C are loaded into the right-most part of D, and we have effectively transferred the left-most bit of E.
This sequence of two instructions is illustrated in Figure 3.18. It can be seen that the bit marked by an X in the most significant position of E will first be transferred into the carry bit, then into the least significant position of D. Effectively, it will have been shifted from E into D.
Fig. 3.18: Shifting from E into D
At this point, referring back to the flowchart of Figure 3.12, we must point to the next bit of MPR and check for the eighth bit. This is accomplished by decrementing the byte counter, contained in register B (see Figure 3.14). The register is decremented by:
DEC B
This is a decrement instruction, which has the obvious effect.
Finally, we must check whether the counter has decremented to the value zero. This is accomplished by checking the value of the Z bit. The reader will recall that the Z (zero) flag indicates whether the previous arithmetic operation (such as a DEC operation) has produced a zero result. However, note that DEC HL, DEC BC, DEC DE, DEC IX, DEC SP do not effect the Z flag. If the counter is not "0", the operation is not finished, and we must execute this loop again. This is accomplished by the next instruction:
JP NZ,MULT
This is a jump instruction which specifies that whenever the Z bit is not set (NZ stands for non-zero), a jump occurs to the location MULT. This is the program loop, which will be executed repeatedly until B decrements to the value 0. Whenever B decrements to the value 0, the Z bit will be set, and the JP NZ instruction will fail. This will result in the next sequential instruction being executed, namely:
LD (RESAD),HL
This instruction merely saves the contents of H and L, i.e., the result of the multiplication, at addres RESAD, the address specified for the result. Note that this instruction will transfer the contents of both registers H and L into two consecutive memory locations, corresponding to the addresses RESAD and RESAD + 1. It saves 16 bits at a time.
| Exercise 3.14: |
Could you write the same multiplication program using the BIT instruction (described in the next chapter) instead of the SRL C instruction? What would be the disadvantage? |
Let us now improve the program, if possible:
| Exercise 3.15: |
Can JR be substituted for JP at the end of the program? If so, what is the advantage? |
| Exercise 3.16: |
Can you use DJNZ to shorten the end of the program? |
Note that, in most cases, the program that we have just developed will be a subroutine and the final instruction will be RET (return). The subroutine will be explained later in this chapter.
This is the first significant program we have encountered so far. It includes many different types of instructions, including transfer instructions (LD), arithmetic instructions (ADD), logical operations (SRL, SLA, RL), and jump operations (JR, JP). It also implements a program loop, in which the lower seven instructions, starting at address MULT, are executed repeatedly. In order to understand programming, it is essential to understand the operation of such a program in complete detail. The program is much longer than the previous simle arithmetic programs we have developed so far, and it should be studied in detail. An important exercise will now be proposed. The reader is strongly urged to do this exercise completely and correctly before proceeding. This will be the only real proof that the concepts presented so far have been understood. If a correct result is obtained, it will mean that you have really understood the mechanism by which the instructions manipulate information in the microprocessor, transfer it between the memory and the registers, and process it. If you not obtain the correct result, or if you do not do this exercise, it is likely that you will experience difficulties later in writing programs yourself. Learning to program requires personal practice. Please pause now, take a piece of paper, or use the illustration of Figure 3.19, and do the following exercise:
| Exercise 3.18: | Every time that a program is written, it should be verified by hand, in order to ascertain that its results will be correct. We are going to do just that: the goal of this exercise is to fill the table of Figure 3.19 completely and accurately. |
Fig. 3.19: Form for Multiplication Exercise
(fill-out form, stored in separate document)
You may want to write directly on Figure 3.19 or make a copy of it. You must determine the contents of every relevant register in the Z80 after the execution of each instruction in the program, from beginning to end. All the registers used by the program of Figure 3.13 are shown in Figure 3.19. From the left to right, they are register B and C, the carry C, registers D and E, and, finally, registers H and L. On the left part of this illustration, fill in the label, if applicable, and then the instructions being executed. On the right of the instructions, fill in the contents of each register after execution of the instruction. Whenever the contents of a register are not known (indefinite), you may want to use dashes to represent its contents. Let us start filling this table together. You will then have to fill out by yourself until the end. The first line appears below:
| LABEL | INSTRUCTION | B | C | C carry |
D | E | H | L |
|---|---|---|---|---|---|---|---|---|
| -- | -- | - | -- | -- | -- | -- | ||
| MPY88 | LD BC,(0200) | 00 | 03 | - | -- | -- | -- | -- |
Fig. 3.20: Multiplication: After One Instruction
We will assume here that we are multiplying "3" (MPR) by "5" (MPD).
The first instruction to be executed is "LD BC, (MPRAD)". The contents of memory location MPRAD is loaded into registers B and C. It has been assumed that MPR is equal to 3, i.e., "00000011". After execution of this instruction, the contents of register C have been set to "3". Note that this instruction will also result in loading register B with whatever followed MPR in the memory. However, the next instruction in the program will take care of this by loading register B with "8", as shown in Figure 3.21. Note that, at this point, the contents of D and E and H and L are still undefined, and this is indicated by the dashes. The LD instruction does not condition the carry bit, so that the contents of the carry bit C are undefined. This is also indicated by a dash.
| LABEL | INSTRUCTION | B | C | C carry |
D | E | H | L |
|---|---|---|---|---|---|---|---|---|
| -- | -- | - | -- | -- | -- | -- | ||
| MPY88 | LD BC,(0200) | 00 | 03 | - | -- | -- | -- | -- |
| LD B,08 | 08 | 03 | - | -- | -- | -- | -- |
Fig. 3.21: Multiplication: After Two Instructions
The situation after execution of the first five instructions of the program (just before the MULT) is shown in Figure 3.22.
| LABEL | INSTRUCTION | B | C | C carry |
D | E | H | L |
|---|---|---|---|---|---|---|---|---|
| -- | -- | - | -- | -- | -- | -- | ||
| MPY88 | LD BC,(0200) | 00 | 03 | - | -- | -- | -- | -- |
| LD B,08 | 08 | 03 | - | -- | -- | -- | -- | |
| LD DE,(0202) | 08 | 03 | - | 00 | 05 | -- | -- | |
| LD D,00 | 08 | 03 | - | 00 | 05 | -- | -- | |
| LD HL,0000 | 08 | 03 | - | 00 | 05 | 00 | 00 |
Fig. 3.22: Multiplication: After Five Instructions
The SRL instruction will perform a logical shift right, and the right-most bit of MPR will fall into the carry bit. You can see in Figure 3.23 that the contents of MPR after the shift is "0000 0001". The carry bit C is now set to "1". The other registers are unchanged by this operation. Please continue to fill out the chart by yourself.
A second iteration is shown at the end of this chapter in Figure 3.41.
| LABEL | INSTRUCTION | B | C | C carry |
D | E | H | L |
|---|---|---|---|---|---|---|---|---|
| -- | -- | - | -- | -- | -- | -- | ||
| MPY88 | LD BC,(0200) | 00 | 03 | - | -- | -- | -- | -- |
| LD B,08 | 08 | 03 | - | -- | -- | -- | -- | |
| LD DE,(0202) | 08 | 03 | - | 00 | 05 | -- | -- | |
| LD D,00 | 08 | 03 | - | 00 | 05 | -- | -- | |
| LD HL,0000 | 08 | 03 | - | 00 | 05 | 00 | 00 | |
| MULT | SRL C | 08 | 01 | 1 | 00 | 05 | 00 | 00 |
| JR NC,0114 | 08 | 01 | 1 | 00 | 05 | 00 | 00 | |
| ADD HL,DE | 08 | 01 | 1 | 00 | 05 | 00 | 05 | |
| NOADD | SLA E | 08 | 01 | 0 | 00 | 0A | 00 | 05 |
| RL D | 08 | 01 | 0 | 00 | 0A | 00 | 05 | |
| DEC B | 07 | 01 | 0 | 00 | 0A | 00 | 05 | |
| JP NZ,010F | 07 | 01 | 0 | 00 | 0A | 00 | 05 |
Fig. 3.23: One Pass Through The Loop
A complete listing showing the contents of all the Z80 registers and the flags is shown in Figure 3.39 at the end of this chapter for the complete multiplication. A hex or decimal listing is shown in Figure 3.40.
The program that we just developed could have been written in many other ways. As a general rule, every programmer can usually find ways to modify, and often improve, a program. For example, we have shifted the multiplicand left before adding. It would have been mathematically equivalent to shift the result one position to the right before adding it to the multiplicand. As a matter of fact, this is an interesting exercise!
The program that we have just developed is a straightforward translation of the algorithm to code. However, effective programming requires close attention to detail, and the length of the program can often be reduced or its execution speed can be improved. We are going to study alternatives designed to improve this basic program.
A first possible improvement lies in the better utilization of the Z80 instruction set. The second-to-last instruction as well as the preceding one can be replaced by a single instruction:
DJNZ MULT
This is a special Z80 "automated jump" which decrements the B register and branches to a specified location if it is not "0". To be absolutely correct, the instruction is not completely identical to the previous pair
DEC B JP NZ,MULT
for it specifies a displacement, and one can only jump within the range of -126 to +129. However, we must here jump to a location which is only a few bytes away, and this improvement is legitimate. The resulting program is shown in Figure 3.24 below:
MPY88 LD DE,(MPDAD)
LD D,0
LD BC,(MPRAD)
LD B,8 BIT COUNTER
LD HL,0
MULT SRL C
JR NC,NOADD
ADD HL,DE
NOADD SLA E
RL D
DJNZ MULT
LD (RESAD),HL
RET
Fig. 3.24: Improved Multiply, Step 1
In order to improve this multiplication program further, we will observe that three different shift operations are used in the initial program of Figure 3.13. The multiplier is shifted right, then the multiplicand MPD is shifted left, in two operations, by first shifting register E left, then rotating register D to the left. This is time-consuming. A standard programming "trick" used in the case of multiplication is based on the following observation: every time that the multiplier is shifted by one bit position, another bit position becomes available in the multiplier register. For example, assuming that the multiplier shifts right (in the previous example), a bit position becomes available on the left. Simultaneously, it can be observed that the first partial product (or "result") will use, at most, 9 bits. If a single register had been allocated to the result in the beginning of the program, we could then use the bit position that has been vacated by the multiplier to store the ninth bit of the result.
After the next shift of MPR, the size of the partial product will be increased by just one bit again. In other words, a single register can be reserverd intially for the partial product, and the bit positions which are being freed by the multiplier can then be used as the MPR is being shifted. In order to improve the program, we are therefore going to assign MPR and RES to a register pair. Ideally, they should be shifted together in a single operation. Unfortunately, the Z80 shifts only 8-bit registers at a time. Like most other 8-bit microprocessors, it has no instruction that allows shifting 16 bits at a time.
However, another trick can be used. The Z80 (like the 8080) is equipped with special 16-bit add instructions that we have already used. Provided that the multiplier and the result are stored in the register pair H and L, we can use the instruction:
ADD HL,HL
which adds the contents of H and L to itself. Adding a number to itself is doubling it. Doubling a number in the binary system is equivalent to a left shift. We have just obtain a 16-bit shift in a single instruction. Unfortunately, the shift occurs to the left when we would like it to occur to the right. This is not a problem.
Conceptually, the MPR can be shifted either left or right. We have used a right shift algorithm because it is the one which is used in ordinary addition. However, it does not necessarily need to be so. The addition operation is communative, and the order can be reversed: shifting the MPR to the left. Therefore, the MPR will reside in register H and the result in register L. The resulting register configuration is shown in Figure 3.25.
Fig. 3.25: Registers for Improved Multiply
The rest of the program is essentially identical to the previous one. The resulting program appears below:
MUL88C LD HL,(MPRAD-1)
LD L,0
LD DE,(MPDAD)
LD D,0
LD B,8 COUNTER
MULT ADD HL,HL SHIFT LEFT
JR NC,NOADD
ADD HL,DE
NOADD DJNZ MULT
LD (RESAD),HL
RET
Fig. 3.26: Improved Multiply, Step 2
When comparing this program to the previous one, it can be seen that the length of the multiplication loop (the number of instructions between MULT and the jump) has been reduced. This program has been written in fewer instructions and this will usually result in faster execution. This shows the advantage of selecting the correct registers to contain the information.
A straightforward design will generally result in a program that works. It will not result in a program that is optimized. It is therefore important to understand and use the available registers and instructions in the best possible way. These examples illustrate a rational approach to register selection and instruction selection for maximum efficiency.
| Exercise 3.22: |
Why did we have to bother zeroing register D when loading MPD into E? |
Finally, let us address a detail which may look irritating to the programmer who is not yet familiar with the Z80. The reader will have noticed that, in order to load MPD into E from memory, we had to load both register D and E at the same time from a memory address. This is because unless the address is contained in register H and L, there is no way to fetch a single byte directly and load it into register E. This is a feature carried over from the early 8008, which had no direct addressing mode. The feature was carried forward in the 8080, with some improvements, and improved still further in the Z80, where it is possible to fetch 16 bits directly from a given memory address (but not 8 bits - except towards register A).
Now, having solved this possible mystery, let us execute a more complex multiplication.
In order to put our newly acquired skills to a test, we will multiply two 16-bit numbers. However, we will assume that the result requires only 16 bits, so that it can be contained in one of the register pairs.
The result, as in our first multiplication example, is contained in registers H and L (see Figure 3.27). The multiplicand is contained in registers D and E.
Fig. 3.27: 16 × 16 Multiply - The Registers
It would be tempting to deposit a multiplier into registers B and C. However, if we want to take advantage of the DJNZ instruction, register B must be allocated to the counter. As a result, half of the multiplier will be in register C, and the other half in register A (see Figure 3.27). The multiplication program appears below:
MUL16 LD A,(MPRAD + 1) MPR, HIGH
LD C,A
LD A,(MPRAD) MPR, LOW
LD B,16D COUNTER
LD DE,(MPDAD) MPD
LD HL,0
MULT SRL C RIGHT SHIFT MPR, HIGH
RRA ROTATE RIGHT MPR, LOW
JR NC,NOADD TEST CARRY
ADD HL,DE ADD MPD TO RESULT
NOADD EX DE,HL
ADD HL,HL DOUBLE - SHIFT LEFT MPD
EX DE,HL
DJNZ MULT
RET
Fig. 3.28: 16 × 16 Multiplication Program
The program is analogous to those we have developed before. The first six instructions (from label MUL16 to label MULT) perform the initialization of registers with the appropriate contents. One complication is introduced here by the fact that the two halves of MPR must be loaded in separate operations. It is assumed that MPRAD points to the low part of MPR in the memory, follow in the next sequential memory location by the high part. (Note that the reverse convention can be used.) Once the high part of MPR has been read into A, it must be transferred into C:
LD A,(MPRAD + 1)
LD C,A
Finally, the low part of MPR can be read directly into the accumulator
LD A,(MPRAD)
The rest of the registers, B, D, E, H, and L, are initialized as usual:
LD B,16D
LD DE,(MPDAD)
LD HL,0
A 16-bit shift must be performed on the multiplier. It requires two separate shift or rotate operations on registers C and A:
MULT SRL C
RRA
After the 16-bit shift, the right-most bit of MPR, i.e., the LSB, is contained in the carry bit C where it can be tested:
JR NC,NOADD
As usual, the multiplicand is not added to the result if the carry bit is "0", and is added to the result if the carry bit is "1":
ADD HL,DE
Next, the multiplicand MPD must be shifted by one position to the left.
However, the Z80 does not have an instruction which will shift the contents of register D and E simultaneously to the left by one bit position, and it can also not add the contents of D and E to itself. The contents of D and E will therefore first be transferred into H and L, then doubled, and transferred back to D and E. This is accomplished by the next three instructions:
NOADD EX DE,HL
ADD HL,HL
EX DE,HL
Finally, the counter B is decremented and a jump occurs to the beginning of the loop as long as it does not decrement to "0":
DJNZ MULT
As usual, it is possible to consider other register allocations which may (or may not) result in shorter codes:
| Exercise 24: |
Referring to the original 16-bit multiplication program of Figure 3.28, can you propose a way to shift the MPD, contained in registers D and E, without transferring it into registers H and L? |
| Exercise 3.25: |
Write a 16-by-16 multiplication program which detects the fact that the result has more than 16 bits. This is a simple improvement of our basic program. |
| Exercise 3.26: |
Write a 16-by-16 multiplication program with a 32-bit result. The suggested register allocation appears in Figure 3.29. Remember that the initial result after the first addition in the loop will require only 16 bits, and that the multiplier will free one bit for each subsequent iteration.
Fig. 3.29: 16 × 16 Multiply with 32-Bit Result |
Let us now examine the last usual arithmetic operation, division.
The algorithm for binary division is analogous to the one which has been used for the multiplication. The divisor is successively subtracted from the high order bits of the dividend. After each subtraction, the result is used instead of the initial dividend. The value of the quotient is simultaneously increased by 1 every time. Eventually, the result of the subtraction is negative. This is called an overdraw. One must then restore the partial result by adding the divisor back to it. Naturally, the quotient must be simultaneously decremented by 1. Quotient and dividend are then shifted by one bit position to the left and the algorithm is repeated. The flowchart is shown in Figure 3.30.
Fig. 3.30: 8-Bit Binary Division Flowchart
The method just described is called the restoring method. A variation of this method which yields an improved speed of execution is called the non-restoring method.
As an example, let us here examine a 16-by-8 division, which will yield an 8-bit quotient and an 8-bit remainder dividend. The register allocation is shown in Figure 3.31.
Fig. 3.31: 16/8 Division - The Registers
The program appears below:
DIV168 LD A,(DVSAD) LOAD DIVISOR
LD D,A INTO D
LD E,0
LD HL,(DVDAD) LOAD 16-BIT DIVIDEND
LD B,8 INITIALIZE COUNTER
DIV XOR A CLEAR C BIT
SBC HL,DE DIVIDEND - DIVISOR
INC HL QUOTIENT = QUOTIENT + 1
JP P,NOADD TEST IF REMAINDER
POSITIVE
ADD HL,DE RESTORE IF NECESSARY
DEC HL QUOTIENT = QUOTIENT - 1
NOADD ADD HL,HL SHIFT DIVIDEND LEFT
DJNZ DIV LOOP UNTIL B = 0
RET
Fig. 3.32: 16/8 Division Program
The first five instructions in the program load the divisor and the dividend respectively into the appropriate registers. They also initialize the counter, in register B, to the value 8. Note again that register B is a preferred location for a counter if the specialized Z80 instruction DJNZ is to used:
DIV168 LD A,(DVSAD)
LD D,A
LD E,0
LD HL,(DVDAD)
LD B,8
Next, the divisor is subtracted from the dividend. Since an SBC instruction must be used (there is no 16-bit subtract without carry), the carry must be set to the value "0" before subtracting. This can be accomplished in a number of ways. The carry can be cleared by performing instructions such as:
Here, an XOR is used:
DIV XOR A
The subtraction can then be performed:
SBC HL,DE
It is anticipated that the subtraction will be successful, i.e., that the remainder will be positive. This is called the "trial subtract" step (refer to the flowchart of Figure 3.30). The quotient is therefore incremented by one. If the subtraction has in fact failed (i.e., if the remainder is negative), the quotient will have to be decremented by one later on:
INC HL
The result of the subtraction is then tested:
JP P,NOADD
If the remainder is positive or zero, the subtraction has been successful, and it is not necessary to restore it. The program jumps to address NOADD. Otherwise, the current dividend must be restored to its previous value, by adding the divisor back to it, and the quotient must be decremented by one. This is performed by the next instructions:
ADD HL,DE
DEC HL
Finally, the resulting dividend is shifted left, in anticipation of the next trial subtract operation. Finally, the B counter is decremented and tested for the value "0". As long as B is not zero, this loop is executed:
NOADD ADD HL,HL
DJNZ DIV
RET
| Exercise 3.27: |
Verify the operation of this division program by hand, by filling out the table of Figure 3.33, as in Exercise 3.18 for the multiplication. Note that the contents of D need not be entered on the form of Figure 3.33, since they are never modified.
Fig. 3.33: Form for Division Program |
The following program uses a restoring method, and leaves a complemented quotient in A. It divides 8 bits by 8 bits (unsigned).
E IS DIVIDEND
C IS DIVISOR
A IS QUOTIENT
B IS REMAINDER
DIV88 XOR A CLEAR ACCUMULATOR
LD B,8 LOOP COUNTER
LOOP88 RL E ROTATE CY INTO ACC-
DIVIDEND
RLA CARRY WILL BE OFF
SUB C TRIAL SUBTRACT DIVISOR
JR NC,$+3 SUBTRACT OK
ADD A,C RESTORE ACCUM, SET CY
DJNZ LOOP88
LD B,A PUT REMAINDER IN B
LD A,E GET QUOTIENT
RLA
CPL COMPLEMENT BITS
RET
Note: the "$" symbol in the sixth instruction represents the value of the program counter.
The following program performs a 16-bit by 15-bit integer division, using a non-restoring technique. IX points to the dividend, IY to the divisor (not zero), (see Figure 3.34).
Fig. 3.34: Non-Restoring Division - The Registers
Register B is used as a counter, initially set to 16.
A and C contain the dividend.
D and E contain the divisor.
H and L contain the result.
The 16-bit dividend is shifted left by:
RL C
RLA
The remainder is shifted left by:
ADC HL,HL
The final quotient is left in B, C, with the remainder in HL. The program follows.
DIV16 LD B,(IX + 1)
LD C,(IX)
LD D,(IY + 1)
LD E,(IY)
LD A,D
OR E (DIVISOR) HIGH OR
(DIVISOR) LOW
JR Z,ERROR CHECK FOR DIVISOR =
ZERO
LD A,B GET (DVD) HI
LD HL,0 CLEAR RESULT
LD B,16D COUNTER
TRIALSB RL C ROTATE RESULT + ACC
RLA LEFT
ADC HL,HL LEFT SHIFT, NEVER SETS
CARRY
SBC HL,DE MINUS DIVISOR
NULL CCF RESULT BIT
JR NC,NGV ACCUMULATOR
NEGATIVE?
PTV DJNZ TRIALSB COUNTER ZERO?
JP DONE
RESTOR RL C ROTATE RESULT + ACC
RLA LEFT
ADC HL,HL AS ABOVE
AND A
ADC HL,DE RESTORE BY ADDING DVSR
JR C,PTV RESULT POSITIVE
JR Z,NULL RESULT ZERO
NGV DJNZ RESTOR COUNTER ZERO?
DONE RL C SHIFT IN RESULT BIT
RLA
LD B,A QUOTIENT IN B,C
LD A,H GET HIGH BYTE OF
REMAINDER
OR A NEGATIVE?
JP P,PREM
ADD HL,DE CORRECT NEGATIVE
REMAINDER
PREM RET
The other class of instructions which can be executed by the ALU inside the microprocessor is the set of logical instructions. They include AND, OR and exclusive OR (XOR). In addition, one can also include here the shift and rotate operations which have already been utilized, and the comparison instruction, called CP for the Z80. The individual use of AND, OR, XOR, will be described in Chapter 4 on the instruction set.
Let us now develop a brief program which will check whether a given memory location called LOC contains the value "0", the value "1", or something else.
The program will introduce the comparison instruction, and performs a series of logical tests. Depending on the result of the comparison, one program segment or another will be executed.
The program appears below:
LD A,(LOC) READ CHARACTER IN
LOC
CP 00H COMPARE TO ZERO
JP Z,ZERO IS IT A 0?
CP 01H COMPARE TO ONE
JP Z,ONE
NONEFOUND ...
ZERO ...
ONE ...
The first instruction: "LD A,(LOC)" reads the contents of memory location LOC, and loads it into the accumulator. This is the character we want to test. It is compared to the value 0 by the following instruction:
CP 00H
This instruction compares the contents of the accumulator to the hexadecimal value "00", i.e., the bit pattern "0000 0000". This comparison instruction will set the Z bit in the flags register to the value "1", if it succeeds. This bit can then be tested by the next instruction:
JP Z,ZERO
The jump instruction tests the value of the Z bit. If the comparison succeeds, the Z bit has been set to one, and the jump will succeed. The program will then jump to the address ZERO. If the test fails, then the next sequential instruction will be executed:
CP 01H
Similarly, the following jump instruction will branch to location ONE if the comparison succeeds. If none of the comparisons succeed, then the instruction at location NONEFOUND will be executed.
JP Z,ONE NONEFOUND ...
This program was introduced to demonstrate the value of the comparison instruction followed by a jump. This combination will be used in many of the following programs.
We have now studied most of the important instructions of the Z80 by using them. We have transferred values between the memory and the registers. We have performed arithmetic and logical operations on such data. We have tested it, and depending on the result of these tests, have executed various portions of the program. In particular, special "automated" Z80 instructions such as DJNZ have been used to shorten programs. Other automated instructions: LDDR, CPIR, INIR will be introduced throughout the remainder of this book.
Full use has been made of special Z80 features, such as 16-bit register instructions to simplify the programs, and the reader should be careful not to use these programs on an 8080: they have been optimized for the Z80.
We have also introduced a structure called a loop. Another important programming structure will be introduced now: the subroutine.
In concept, a subroutine is simply a block of instructions which has been given a name by the programmer. From a practical standpoint, a subroutine must start with a special instruction called a subroutine declaration, which identifies it as such for the assembler. It is also terminated by another special instruction called a return. Let us first illustrate the use of a subroutine in a program in order to demonstrate its value. Then, we will examine how it is actually implemented.
Fig. 3.35: Subroutine Calls
The use of a subroutine is illustrated in Figure 3.35. The main program appears on the left of the illustration. The subroutine is shown symbolically on the right. Let us examine the subroutine mechanism. The lines of the main program are executed successively until a new instruction "CALL SUB" is met. This special instruction is the subroutine call and results in a transfer to the subroutine. This means that the next instruction to be executed after CALL SUB is the first instruction within the subroutine. This is illustrated by arrow 1 on the illustration.
Then, the subprogram within the subroutine executes just like any other program. We will assume that the subroutine does not contain any other calls. The last instruction of this subroutine is a RETURN. This is a special instruction which will cause a return to the main program. The next instruction to be executed after the RETURN is the one following the CALL SUB in the main program. This is illustrated by arrow 3 on the illustration. Program execution continues then, as illustrated by arrow 4.
In the body of the main program a second CALL SUB appears. A new transfer occurs, shown by arrow 5. This means that the body of the subroutine is again executed following the CALL SUB instruction.
Whenever the RETURN within the subroutine is encountered, a return occurs to the instruction following the CALL SUB in question. This is illustrated by arrow 7. Following the return to the main program, program execution proceeds normally, as illustrated by arrow 8.
The effect of the two special instructions CALL SUB and RETURN should now be clear. What is the value of the subroutine mechanism?
The essential value of the subroutine is that it can be called from any number of points in the main program, and used repeatedly without rewriting it. A first advantage is that this approach saves memory space, since ther is no need to rewrite the subroutine every time. A second advantage is that the programmer can design a specific subroutine only once and then use it repeatedly. This is a significant simplification in program design.
We will examine here how the two special instructions, CALL SUB and RETURN, are implemented internally within the processor. The effect of the CALL SUB instruction is to cause the next instruction to be fetched at a new address. You will remember (or else read Chapter 1 again) that the address of the next instruction to be executed in a computer is contained in the program counter (PC). This means that the effect of the CALL SUB is to substitute new contents in register PC. Its effect is to load the start address of the subroutine in the program counter. Is that really sufficient?
To answer this question, let us consider the other instruction which has to be implemented: the RETURN. The RETURN must cause, as its name indicates, a return to the instruction that follows the CALL SUB. This is possible only if the address of this instruction has been preserved somewhere. This address happens to be the value of the program counter at the time that the CALL SUB was encountered. This is because the program counter is automatically incremented every time it is used (read Chapter 1 again). This is precisely the address that we want to preserve, so that we can later perform the RETURN.
The next problem is: where can we save this return address? This address must be saved in a location where it is guaranteed that it will not be erased.
However, let us now consider the following situation, illustrated by Figure 3.36. In this example, subroutine 1 contains a call to SUB2. Our mechanism should work in this case as well. Naturally, there might even be more than two subroutines, say N "nested" calls. Whenever a new CALL is encountered, the mechanism must therefore again store the program counter. This implies that we need at least 2N memory locations for this mechanism. Additionally, we will need a structure which can preserve the chronological ordering in which addresses have been saved.
The structure has a name and has already been introduced. It is the stack. Figure 3.38 shows the actual contents of the stack during successive subroutine calls. Let us look at the main program first. At address 100, the first call is encountered: CALL SUB1. We will assume that, in this microprocessor, the subroutine call uses 3 bytes (RST is an exception). The next sequential address is therefore not "101", but "103". The CALL instruction uses addresses "100", "101", "102". Because of the control unit of the Z80 "knows" that it is a 3-byte instruction, the value of the program counter, when the call has been completely decoded, will be "103". The effect of the call will be to load the value "280" in the program counter. "280" is the starting address of SUB1.
Fig. 3.36: Nested Calls
We are now ready to demonstrate the effect of the RETURN instruction and the correct operation of our stack mechanism. Execution proceeds within SUB2 until the RETURN instruction is encountered at time 3. The effect of the RETURN instruction is simply to pop the top of the stack into the program counter. In other words, the program counter is restored to its value prior to the entry into the subroutine. The top of the stack in our example is "303". Figure 3.38 shows that, at time 3, value "303" has been removed from the stack and has been put back into the program counter. As a result, instruction execution proceeds from address "303". At time 4, the RETURN of SUB1 is encountered. The value on top of the stack is "103". It is popped and is installed in the program counter. As a result, program execution will proceed from location "103" on within the main program. This is, indeed, the effect we wanted. Figure 3.38 shows tat at time 4 the stack is again empty. The mechanism works.
The subroutine call mechanism works up to the maximum dimension of the stack. This is why early microprocessors which had a 4- or 8-register stack were essentially limited to 4 or 8 levels of subroutine calls.
Note that, on Figures 3.36 and 3.37, the subroutines have been shown to the right of the main program. This is only for the clarity of the diagram. In reality, the subroutines are typed by the user as regular instructions of the program. On a sheet of paper, when producing the listing of the complete program, the subroutines may be at the beginning of the text, in its middle, or at the end. This is why they are proceded by a subroutine declaration: they must be identified. The special instructions tell the assembler that what follows should be treated as a subroutine. Such assembler directives will be discussed in Chapter 10.
Fig. 3.37: The Subroutine Calls
Fig. 3.38: Stack vs. Time
The basic concept relating to subroutines have now been presented. It has been shown that the stack is required in order to implement this mechanism. The Z80 is equipped with a 16-bit stack-pointer register. The stack can therefore reside anywhere within the memory and may have up to 64K (1K=1024) bytes, assuming they are available for that purpose. In practice, the start address for the stack, as well as its maximum dimension, will be defined by the programmer before writing his program. A memory area will then be reserved for the stack.
The subroutine-call instruction, in the case of the Z80, is called CALL, and comes in two versions; the direct or unconditional call, such as CALL ADDRESS, is the one we have already described. In addition, the Z80 is equipped with a conditional call instruction which will call a subroutine if a condition is met. For example: CALL NZ,SUB1 will result in a call to subroutine 1 if the Z flag is zero at the time of the test. This is a powerful facility, since many subroutine calls are conditional, i.e., occur only if some specific condition is met.
CALL CC,NN is executed only if the condition specified by "CC" is true. CC is a set of three bits (bits 3, 4 and 5 of the opcode) which may specify up to eight conditions. They correspond respectively to the four flags "Z", "C", "P/V", "S" being either zero or non-zero.
Similarly, two types of return instructions are provided: RET and RET CC.
RET is the basic return instruction. It occupies one byte, and causes the top two bytes of the stack to be re-installed in the program counter. It is unconditional.
RET CC has the same effect except that it is executed only if the conditions specified by CC are true. The condition bits are the same as for the CALL instructions just described.
Additionally, two specilized types of return are available which are used to terminate interrupt routines: RETI, RETN. They are described in the section on the Z80 instructions as well as in the section on interrupts.
Finally, one more specilized instruction is provided which is analogous to a subroutine call, but allows the program to branch to only one of eight starting locations in page zero. This is the RST P instruction. This is a one-byte instruction which automatically preserves the program counter in the stack, and causes a branch to the address specified by the three-bit P field. The P field corresponds to bits 3,4 and 5 of the instruction, multiplied by eight.
In other words, if bits 3, 4, 5 are "000", the jump will occur to location 00H. If the bits are "001", the branch will occur to 08H, etc. up to 111, which will cause a branch to location 38H. The RST instruction is very efficient in terms of speed since it is a single-byte instruction. However, it can jump to only eight locations, in page 0. Additionally, these addresses in page 0 are only eight bytes apart. This instruction is a carry-over from the 8080 and was extensively used for interrupts. This will be described in the interrupt section. However, this instruction may be used for any other purpose by the programmer, and should be considered a possible specilized subroutine call.
Most of the programs that we have developed and are going to develop would usually be written as subroutines. For example, the multiplication program is likely to be used by many areas of the program. In order to facilitate and clarify program development, it is therefore convenient to define a subroutine whose name would be, for example, MULT. At the end of this subroutine we would simply add the instruction RET.
| Exercise 3.32: | If MULT is used as a subroutine, would it "damage" any internal flags or registers? |
Recursion is a word used to indicate that a subroutine is calling itself. If have understood the implementation mechanism, you should now be able to answer the following question:
| Exercise 3.33: | Is it legal to let a subroutine to call itself? (In other words, will everything work even if a subroutine calls itself?) If you are not sure, draw the stack and fill it with the successive addresses. Then, look at the registers and memory (see Exercise 3.18) and determine if a problem exists. |
Interrupts will be discussed in the input/output chapter (Chapter 6). All returns except returns from interrupts are one-byte instructions; all calls are 3-byte instructions (except RST).
When calling a subroutine, one normally expects the subroutine to work on some data. For example, in the case of multiplication, one wants to transmit two numbers to the subroutine which will perform the multiplication. We saw in the case of the multiplication routine that this subroutine expected to find the multiplier and the multiplicand in given memory locations. This illustrates one method of passing parameters: through memory. Two other techniques are used, so that we have three ways of passing parameters.
Registers can be used to pass parameters. This is an advantageous solution, provided that the registers are available, since one does not need to use a fixed memory location: the subroutine remains memory-independent. If a fixed memory location is used, any other user of the subroutine must be very careful that he uses the same convention and that the memory location is indeed available (look at Exercise 3.19 above). This is why, in many cases, a block of memory locations is reserved simply to pass parameters among various subroutines.
Using memory has the advantage of greater flexibility (more data), but results in poorer performance and also in tying a subroutine to a given memory area.
Depositing parameters in the stack has the same advantage as using registers: it is memory-independent. The subroutine simply knows that it is supposed to receive, say, two parameters which are stored on top of the stack. Naturally, it has disadvantages: it clutters the stack with data and, therefore, reduces the number of possible levels of subroutine calls. It also significantly complicates the use of the stack, and may require multiple stacks.
The choice is up to the programmer. In general, one wishes to remain independent from actual memory locations as long as possible.
If registers are not available, a possible solution is the stack. However, if a large quantity of information should be passed to a subroutine, this information may have to reside directly in the memory. An elegant way around the problem of passing a block of data is simply to transmit a pointer to the information. A pointer is the address of the beginning of the block. A pointer can be transmitted in a register, or in the stack (two stack locations can be used to store a 16-bit address), or in a given memory location(s).
Finally, if neither of the two solutions is applicable, then an agreement may be made with the subroutine that the data will be at some fixed memory location (the "mail-box").
| Exercise 3.35: | Which of the three methods above is best for recursion? |
There is a strong advantage to structuring portions of a program into identifiable subroutines: they can be debugged independently and can have a mnemonic name. Provided they will be used in other areas of the program, they become shareable, and one can thus build a library of useful subroutines. However, there is no general panacea in computer programming. Using subroutines systematically for any group of instructions that can be grouped by function may also result in poor efficiency. The alert programmer will have to weigh the advantages against the disadvantages.
This chapter has presented the way information is manipulated inside the Z80 by instructions. Increasingly complex algorithms have been introduced and translated into programs. The main types of instructions have been used and explained.
Important structures as loops, stacks and subroutines, have been defined.
You should now have acquired a basic understanding of programming, and of the major techniques used in standard applications. Let us study the instructions available.
A=00 BC=0000 DE=0000 HL=0000 S=0300 P=0100 0100' LD BC,(0200)
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0200')
A=00 BC=0003 DE=0000 HL=0000 S=0300 P=0104 0104' LD B,08
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
A=00 BC=0803 DE=0000 HL=0000 S=0300 P=0106 0106' LD DE,(0202)
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0202')
A=00 BC=0803 DE=0005 HL=0000 S=0300 P=010A 010A' LD D,00
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
A=00 BC=0803 DE=0005 HL=0000 S=0300 P=010C 010C' LD HL,0000
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0000')
A=00 BC=0803 DE=0005 HL=0000 S=0300 P=010F 010F' SRL C
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
C A=00 BC=0801 DE=0005 HL=0000 S=0300 P=0111 0111' JR NC,0114
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0114')
C A=00 BC=0801 DE=0005 HL=0005 S=0300 P=0113 0113' ADD HL,DE
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
A=00 BC=0801 DE=0005 HL=0005 S=0300 P=0114 0114' SLA E
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
V A=00 BC=0801 DE=000A HL=0005 S=0300 P=0116 0116' RL D
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0801 DE=000A HL=0005 S=0300 P=0118 0118' DEC B
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
N A=00 BC=0701 DE=000A HL=0005 S=0300 P=0119 0119' JP NZ,010F
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (010F')
N A=00 BC=0701 DE=000A HL=0005 S=0300 P=010F 010F' SRL C
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V C A=00 BC=0700 DE=000A HL=0005 S=0300 P=0111 0111' JR NC,0114
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0114')
Z V C A=00 BC=0700 DE=000A HL=0005 S=0300 P=0113 0113' ADD HL,DE
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0700 DE=000A HL=000F S=0300 P=0114 0114' SLA E
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
V A=00 BC=0700 DE=0014 HL=000F S=0300 P=0116 0116' RL D
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0700 DE=0014 HL=000F S=0300 P=0118 0118' DEC B
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
N A=00 BC=0600 DE=0014 HL=000F S=0300 P=0119 0119' JP NZ,010F
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (010F')
N A=00 BC=0600 DE=0014 HL=000F S=0300 P=010F 010F' SRL C
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0600 DE=0014 HL=000F S=0300 P=0111 0111' JR NC,0114
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0600 DE=0014 HL=000F S=0300 P=0114 0114' SLA E
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
V A=00 BC=0600 DE=0028 HL=000F S=0300 P=0116 0116' RL D
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0600 DE=0028 HL=000F S=0300 P=0118 0118' DEC B
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
N A=00 BC=0500 DE=0028 HL=000F S=0300 P=0119 0119' JP NZ,010F
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (010F')
N A=00 BC=0500 DE=0028 HL=000F S=0300 P=010F 010F' SRL C
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0500 DE=0028 HL=000F S=0300 P=0111 0111' JR NC,0114
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0114')
Z V A=00 BC=0500 DE=0028 HL=000F S=0300 P=0114 0114' SLA E
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
V A=00 BC=0500 DE=0050 HL=000F S=0300 P=0116 0116' RL D
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0500 DE=0050 HL=000F S=0300 P=0118 0118' DEC B
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
N A=00 BC=0400 DE=0050 HL=000F S=0300 P=0119 0119' JP NZ,010F
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (010F')
N A=00 BC=0400 DE=0050 HL=000F S=0300 P=010F 010F' SRL C
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0400 DE=0050 HL=000F S=0300 P=0111 0111' JR NC,0114
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0114')
Z V A=00 BC=0400 DE=0050 HL=000F S=0300 P=0114 0114' SLA E
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
S V A=00 BC=0400 DE=00A0 HL=000F S=0300 P=0116 0116' RL D
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0400 DE=00A0 HL=000F S=0300 P=0118 0118' DEC B
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
N A=00 BC=0300 DE=00A0 HL=000F S=0300 P=0119 0119' JP NZ,010F
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (010F')
N A=00 BC=0300 DE=00A0 HL=000F S=0300 P=010F 010F' SRL C
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0300 DE=00A0 HL=000F S=0300 P=0111 0111' JR NC,0114
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0114')
Z V A=00 BC=0300 DE=00A0 HL=000F S=0300 P=0114 0114' SLA E
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
C A=00 BC=0300 DE=0040 HL=000F S=0300 P=0116 0116' RL D
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
A=00 BC=0300 DE=0140 HL=000F S=0300 P=0118 0118' DEC B
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
N A=00 BC=0200 DE=0140 HL=000F S=0300 P=0119 0119' JP NZ,010F
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (010F')
N A=00 BC=0200 DE=0140 HL=000F S=0300 P=010F 010F' SLR C
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0200 DE=0140 HL=000F S=0300 P=0111 0111' JR NC,0114
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0114')
Z V A=00 BC=0200 DE=0140 HL=000F S=0300 P=0114 0114' SLA E
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
S A=00 BC=0200 DE=0280 HL=000F S=0300 P=0116 0116' RL D
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
A=00 BC=0200 DE=0180 HL=000F S=0300 P=0118 0118' DEC B
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
N A=00 BC=0100 DE=0280 HL=000F S=0300 P=0119 0119' JP NZ,010F
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (010F')
N A=00 BC=0100 DE=0180 HL=000F S=0300 P=010F 010F' SRL C
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V A=00 BC=0100 DE=0280 HL=000F S=0300 P=0111 0111' JR NC,0114
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0114')
Z V A=00 BC=0100 DE=0280 HL=000F S=0300 P=0114 0114' SLA E
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z V C A=00 BC=0100 DE=0200 HL=000F S=0300 P=0116 0116' RL D
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
V A=00 BC=0100 DE=0500 HL=000F S=0300 P=0118 0118' DEC B
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Z N A=00 BC=0000 DE=0500 HL=000F S=0300 P=0119 0119' JP NZ,010F
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (010F')
Z N A=00 BC=0000 DE=0500 HL=000F S=0300 P=011C 011C' LD (0204),HL
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00 (0204')
Z N A=00 BC=0000 DE=0500 HL=000F S=0300 P=011F 011F' NOP
A'=00 B'=0000 D'=0000 H'=0000 X=0000 Y=0000 I=00
Fig. 3.39: Multiplication: A Complete Trace
CROMEMCO CDOS Z80 ASSEMBLER version 02.15 PAGE 0001
0000' 0001 ORG 0100H
(0200) 0002 MPRAD DL 0200H
(0202) 0003 MPDAD DL 0202H
(0204) 0004 RESAD DL 0204H
0005 ;
0100 ED4B0002 0006 MP488 LD BC,(MPRAD) ;LOAD MULTIPLIER INTO C
0104 0608 0007 LD B,8 ;B IS BIT COUNTER
0106 ED5B0202 0008 LD DE,(MPDAD) ;LOAD MULTIPLICAND INTO E
010A 1600 0009 LD D,0 ;CLEAR D
010C 210000 0010 LD HL,0 ;SET RESULT TO 0
010F CB39 0011 MULT SRL C ;SHIFT MULTIPLIER BIT INTO CARRY
0111 3001 0012 JR NC,NOADD ;TEST CARRY
0113 19 0013 ADD HL,DE ;ADD MPD TO RESULT
0114 CB23 0014 NOADD SLA E ;SHIFT MPD LEFT
0116 CB12 0015 RL D ;SAVE BIT IN D
0118 05 0016 DEC B ;DECREMENT SHIFT COUNTER
0119 C20F01 0017 JP NZ,MULT ;DO IT AGAIN IF COUNTER <> 0
011C 220402 0018 LD (RESAD),HL ;STORE RESULT
011F (0000) 0019 END
Errors 0
Fig. 3.40: The Multiplication Program (Hex)
| LABEL | INSTRUCTION | B | C | C carry |
D | E | H | L |
|---|---|---|---|---|---|---|---|---|
| -- | -- | - | -- | -- | -- | -- | ||
| MPY88 | LD BC,(0200) | 00 | 03 | - | -- | -- | -- | -- |
| LD B,08 | 08 | 03 | - | -- | -- | -- | -- | |
| LD DE,(0202) | 08 | 03 | - | 00 | 05 | -- | -- | |
| LD D,00 | 08 | 03 | - | 00 | 05 | -- | -- | |
| LD HL,0000 | 08 | 03 | - | 00 | 05 | 00 | 00 | |
| MULT | SRL C | 08 | 01 | 1 | 00 | 05 | 00 | 00 |
| JR NC,0114 | 08 | 01 | 1 | 00 | 05 | 00 | 00 | |
| ADD HL,DE | 08 | 01 | 1 | 00 | 05 | 00 | 05 | |
| NOADD | SLA E | 08 | 01 | 0 | 00 | 0A | 00 | 05 |
| RL D | 08 | 01 | 0 | 00 | 0A | 00 | 05 | |
| DEC B | 07 | 01 | 0 | 00 | 0A | 00 | 05 | |
| JP NZ,010F | 07 | 01 | 0 | 00 | 0A | 00 | 05 | |
| MULT | SRL C | 07 | 00 | 1 | 00 | 0A | 00 | 05 |
| JR NC,0114 | 07 | 00 | 1 | 00 | 0A | 00 | 05 | |
| ADD HL,DE | 07 | 00 | 0 | 00 | 0A | 00 | 0F | |
| NOADD | SLA E | 07 | 00 | 0 | 00 | 14 | 00 | 0F |
| RL D | 07 | 00 | 0 | 00 | 14 | 00 | 0F | |
| DEC B | 06 | 00 | 0 | 00 | 14 | 00 | 0F | |
| JP NZ,010F | 06 | 00 | 0 | 00 | 14 | 00 | 0F |
Fig. 3.41: Two Iterations Through the Loop